Laplace Transform Calculator

Introduction to Laplace Transform Calculator

The Laplace Transform Calculator is an online tool that helps users instantly compute Laplace transforms of mathematical functions. Instead of solving lengthy integrals by hand, anyone can enter their function into the input field, use the on-screen keypad for operators and symbols and press Calculate to get the result.

This tool is designed for students, engineers, and professionals who regularly deal with differential equations, signal processing and system analysis. It eliminates manual errors and saves valuable time by providing accurate Laplace transforms in seconds.

Whether the function involves polynomials, trigonometric terms, exponential expressions or logarithms, the calculator ensures reliable outputs, making it a must-have for anyone working with Laplace transforms.

How to Use the Laplace Transform Calculator?

The calculator is designed with a simple and user-friendly interface so anyone can compute Laplace transforms instantly. Here’s how users can make the most of it:

• Enter the function: Type the function directly into the input field. The calculator supports polynomials, exponentials, trigonometric, logarithmic, and root functions.
• Use the keypad: If preferred, the on-screen keypad can be used to insert operators, powers and mathematical symbols with ease.
• Click Calculate: Press the CALCULATE button to process the function.
• View the result: The solution will appear in the result box, showing the transformed function in terms of s.
• Re-calculate if needed: If a mistake is made or a new function needs to be checked, simply adjust the input and calculate again.

One important point to remember is that this tool is built only for direct Laplace transforms and does not solve inverse transforms or definite integrals.

What Is the Laplace Transform?

The Laplace transform is a mathematical technique that converts a time-domain function f(t) into a frequency-domain representation F(s). This transformation is extremely valuable because it simplifies the process of solving complex differential equations, which are common in engineering, physics, and applied mathematics.

Unlike the Fourier Transform, which is primarily used to analyze stable and periodic signals in the frequency domain, the Laplace Transform can handle both stable and unstable functions and is particularly useful for solving differential equations with initial conditions. In practical terms, the Laplace transform allows users to work with algebraic equations instead of calculus-based problems, making calculations easier and faster. Functions involving exponentials, trigonometric identities, or polynomials become much more manageable once transformed.

Formula for Laplace Transform

The general formula for the Laplace Transform of a function f(t), where t ≥ 0, is:

$$ F(s) = \int_0^{\infty} e^{-st} f(t)\, dt $$

Here:

• f(t) is the original function in the time domain.
• F(s) is the transformed function in the frequency domain.
• s is a complex variable, usually expressed as s=σ+jω.

Unlike a standard definite integral where the limits are fixed between two values, the Laplace transform integrates from 0 to ∞ with an exponential factor.

How To Find the Laplace Transform of a Function?

To find the Laplace Transform of a function, the process generally involves applying the standard formula:

$$ F(s) = \int_0^{\infty} e^{-st} f(t)\, dt $$

Here’s a step-by-step approach to determine it manually:

• Identify the function f(t): Start with the given time-domain function (e.g., constant, polynomial, exponential, or trigonometric).
• Apply the Laplace transform formula: Substitute the function into the integral form.
• Simplify the exponential expression: Multiply f(t) by e^{-st}.
• Evaluate the integral: Solve the integral from 0 to infinity.
• Obtain the frequency-domain function F(s): This is the Laplace transform of the original function.

For example, if f(t) = e^2t, then:

$$ F(s) = \int_0^{\infty} e^{-st} e^{2t}\, dt = \int_0^{\infty} e^{-(s-2)t}\, dt = \frac{1}{s-2} $$

The key point is that many users prefer using a Laplace transform table instead of solving every integral from scratch, especially for more complex functions.

Laplace Transform Table

The Laplace transform table is given here: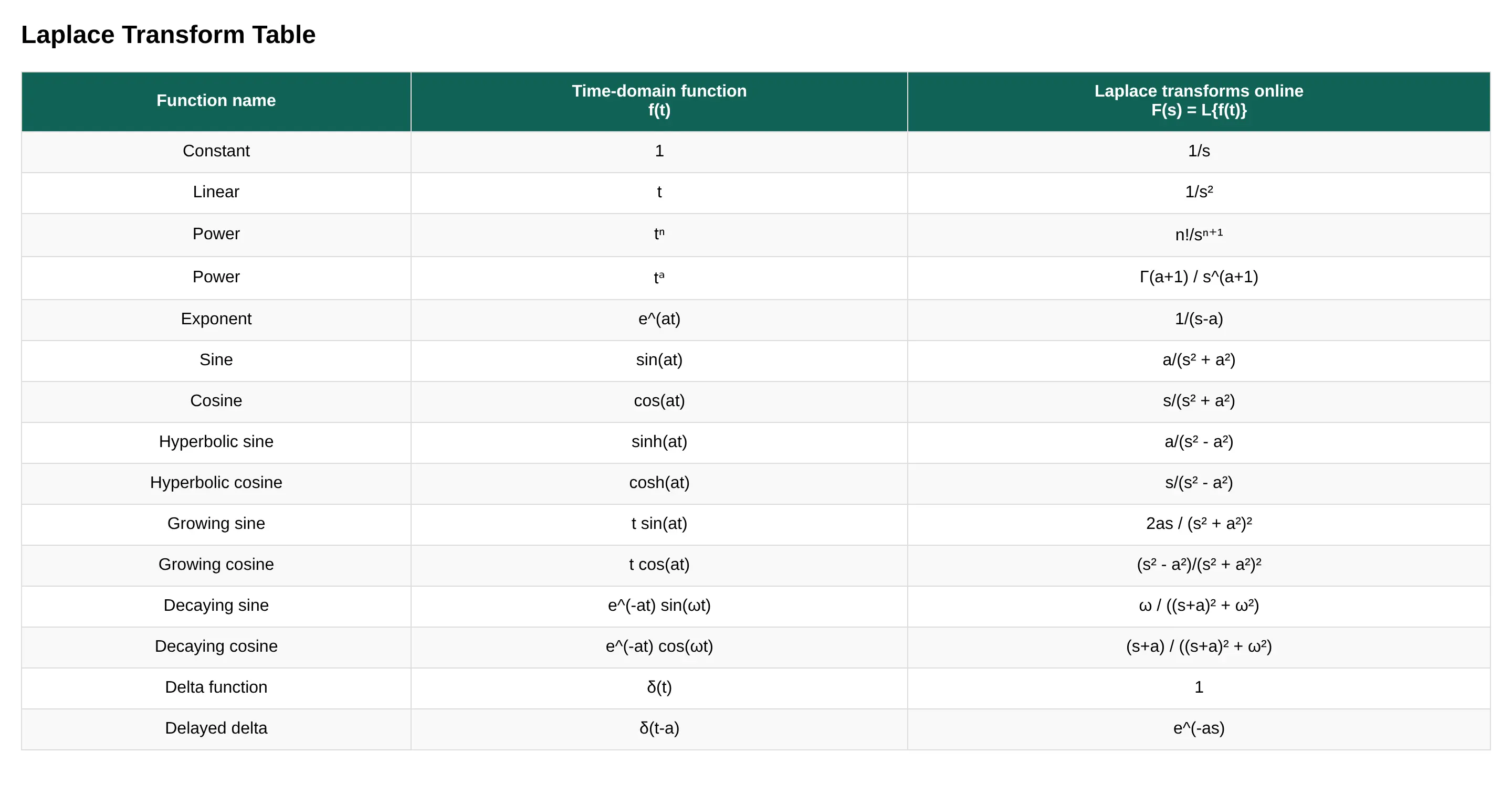

Solved Example of Laplace Transform

To better understand how the Laplace transform works, let’s look at a few solved examples:

Example 1:

$$ \text{Constant function} \; f(t) = 1 $$

Write the definition:

$$ F(s) = \int_0^\infty e^{-st} f(t)\, dt $$

Substitute function f(t) = 1:

$$ F(s) = \int_0^\infty e^{-st} (1)\, dt $$

Integrate:

$$ F(s) = \left[ \frac{e^{-st}}{-s} \right]_0^\infty $$

Simplify:

$$ F(s) = \frac{1}{s}, \quad s > 0 $$

So, the Laplace transform of a function f(t) = 1 is:

$$ F(s) = \frac{1}{s} $$

Example 2:

$$ \text{Exponential function} \; f(t) = e^{2t} $$

Formula:

$$ F(s) = \int_0^\infty e^{-st} f(t)\, dt $$

Substitute f(t) = e^{2t}:

$$ F(s) = \int_0^\infty e^{-st} e^{2t}\, dt $$

Simplify inside:

$$ F(s) = \int_0^\infty e^{-(s-2)t}\, dt $$

Apply integration rule:

$$ F(s) = \frac{1}{s-2}, \quad s > 2 $$

Example 3:

$$ \text{Trigonometric function} \; f(t) = \sin(t) $$

Start with the formula:

$$ F(s) = \int_0^\infty e^{-st} f(t)\, dt $$

Substitute f(t) = sin(t):

$$ F(s) = \int_0^\infty e^{-st} \sin(t)\, dt $$

Use the standard identity for integrating exponentials with sine:

$$ \int e^{ax}\sin(bx)\, dx = \frac{e^{ax}(a\sin(bx) - b\cos(bx))}{a^2 + b^2} $$

Here, a = -s, b = 1

Apply the formula:

$$ \int e^{-st}\sin(t)\, dt = \frac{e^{-st}((-s)\sin(t) - \cos(t))}{s^2 + 1} $$

Now apply limits from 0 to ∞:

As t → ∞, 𝑒^−𝑠𝑡 → 0 (since 𝑠 > 0).

At t = 0

$$ \frac{e^{0}((-s)\sin(0) - \cos(0))}{s^2 + 1} = \frac{0 - 1}{s^2 + 1} = \frac{-1}{s^2 + 1} $$

Subtract values:

$$ F(s) = 0 - \left( \frac{-1}{s^2 + 1} \right) $$

Final Answer:

$$ F(s) = \frac{1}{s^2 + 1}, \quad s > 0 $$

Key Features of Our Laplace Calculator

The Laplace transform calculator at IntegralSolver.net is designed to provide quick, accurate, and step-by-step solutions for users working with Laplace transforms. Some of the standout features include:

• Step-by-Step Solutions: The calculator not only gives the final Laplace transform of a function, but also shows the intermediate steps, making it easier for learners to follow the process.
• Handles a Wide Range of Functions: Whether it’s exponential, polynomial, trigonometric, or constant functions, the tool can compute their Laplace transforms efficiently.
• Instant Results: Users can simply input their function and get results in seconds, saving valuable time compared to manual calculations.
• User-Friendly Interface: The clean and simple layout allows even beginners to compute transforms without confusion.
• Accurate Mathematical Computation: Built with advanced algorithms, the tool ensures precision in every calculation.
• Free Online Access: There’s no need to download software or sign up. The calculator is available online anytime.

This combination of speed, accuracy, and simplicity makes the calculator an essential tool for students, engineers, and professionals dealing with Laplace transforms in their work.

Benefits of Using Our Online Laplace Transform Calculator

Using the Laplace calculator comes with multiple advantages that make it a go-to tool for students, educators, and professionals:

• Saves Time: Manual calculations of Laplace transforms can be lengthy and prone to mistakes. With this tool, users get instant results without the hassle.
• Accuracy Guaranteed: The calculator eliminates human error, ensuring precise answers every time.
• Learning Aid: Since the tool provides step-by-step solutions, it helps learners understand the process behind solving transforms, not just the final result.
• Works on Various Functions: From simple constants to complex trigonometric and exponential expressions, the calculator handles them all.
• Accessible Anytime, Anywhere: Being a web-based tool, it can be accessed from any device without installation.
• Helpful for Practice: Students preparing for exams can quickly test different functions and verify their solutions using the calculator.

When to Use the Laplace Calculator?

The calculator is especially useful in situations where manual solving would be time-consuming or complex. Here are the common cases when this tool should be used:

• Verifying Homework or Assignments: Students can quickly confirm whether their manually solved answers are correct.
• Learning New Concepts: Beginners who are just introduced to Laplace transforms can use the calculator to see worked-out steps and build confidence.
• Handling Complex Functions: When the function involves exponentials, trigonometric terms, or higher-degree polynomials, the tool simplifies the process.
• Saving Time in Exam Preparation: Instead of spending long hours on repeated calculations, students can practice more problems efficiently.
• Professional Use: Engineers and researchers who apply Laplace transforms in control systems, signal processing, and physics can save time by using the calculator for quick computations.

When the goal is to convert time-domain functions to the frequency domain, this tool is best. For reverse problems, an Inverse Laplace Transform Calculator may be more suitable.

Conclusion

The Laplace transform calculator is a reliable online tool that simplifies the process of finding the Laplace transform of a function. By offering step-by-step solutions, handling a variety of functions, and delivering accurate results instantly, it serves as a practical resource for students, teachers, and professionals alike.

Whether the goal is to learn, verify answers, or save time on complex problems, this calculator ensures a smooth and error-free experience. With its user-friendly design and accessibility, it makes solving Laplace transforms easier than ever before.

Jack Bowater

Last Update
Friday 3, 2025

   

About Author

Jack Bowater is an expert in calculus with years of experience in integration, derivatives, and advanced math. He teaches complex topics in simple ways to help students learn faster. Jack aims to make calculus easy and clear so readers feel confident solving problems independently. His step-by-step approach helps students understand and apply calculus concepts effectively for exams or building math skills.